When Machine Learning Meets Social Science: A Comparative Study of Ordinary Least Square, Stochastic Gradient Descent, and Support Vector Regression for Exploring the Determinants of Behavioral Intentions to Tuberculosis Screening
Copyright ⓒ 2022 by the Korean Society for Journalism and Communication Studies
Abstract
Regression analysis is one of the most widely utilized methods because of its adaptability and simplicity. Recently, the machine learning (ML) approach, which is one aspect of regression methods, has been gaining attention from researchers, including social science, but there are only a few studies that compared the traditional approaches with the ML approach. This study was conducted to explore the usefulness of the ML approach by comparing the ordinary least square estimate (OLS), the stochastic gradient descent algorithm (SGD), and the support vector regression (SVR) with a model predicting and explaining the tuberculosis screening intention. The optimized models were evaluated by four aspects: computational speed, effect and importance of individual predictor, and model performance. The result demonstrated that each model yielded a similar direction of effect and importance in each predictor, and the SVR with the radial kernel had the finest model performance compared to its computational speed. Finally, this study discussed the usefulness and attentive points of the ML approach when a researcher utilizes it in the field of communication.
Keywords:
ordinary least square, stochastic gradient descent, support vector regression, determinants of tuberculosis screening intentionScientific research is a process that describes, predicts, and explains or understands natural or social phenomena of interest in the world. This process includes, as Lynch (2013) mentions, “developing an empirically answerable question, deriving a falsifiable hypothesis from a theory to answer the question, collecting (or finding) and analyzing empirical data to test the hypothesis, rejecting or failing to reject the hypothesis, and relating the results of the analyses back to the theory from which the question was drawn” (p. 5). Given that statistics is a way of organizing, describing, and making inferences from data (Hayes, 2005), no one can deny that it is an essential part of the scientific process. In particular, regression analysis has not only played an important role in the scientific process since Sir Francis Galton (1886) published his famous article, “Regression Towards Mediocrity in Hereditary Stature,” but has also become the most popular statistical analysis method in all fields of social science as well as natural science. In fact, as Fox (1991) notes, no statistical technique has been used more than regression analysis in the field of social science. Such pervasive use of regression analysis stems from the fact that regression analysis is extraordinarily useful for predicting and explaining phenomena of interest through the estimation of the model (Ethington et al., 2002).
Since Galton (1886) introduced the general technique of regression, regression analysis has continuously evolved, and its applicability has expanded along with its evolutionary changes. The authors pay close attention to the use of advanced computational techniques, such as the machine learning (ML) approach in particular, for regression analysis. ML is not only one of the fastest-growing fields in computer science, but many other fields have adopted ML methods to analyze data or otherwise support their research domains (Chen et al., 2018). The use of statistical modeling can be classified into two cultures (Breiman, 2001), where the traditional regression approach and ML approach represent data modeling culture and algorithm modeling culture, respectively. Although the traditional statistical approach to regression is fundamentally different from the ML-based approach in terms of scientific philosophies, purposes, and practices, using ML methods for regression analysis continues to gain popularity in the field of physical and natural science (e.g., Niu et al., 2019). In the field of social science, discussions on the use of ML have also increased as a better alternative to traditional regression analysis (e.g., Buskirk et al., 2018; Grimmer et al., 2021; Hindman, 2015; Rudin, 2015). There are very few studies, however, that discuss the utility of ML methods in the field of social science through empirical comparisons between these two approaches in regards to statistical modeling such as model performance, predictive performance, and optimization technique.
The main purpose of this study is to explore the usefulness of ML-based regression in the field of social science. By doing so, the authors empirically compare ordinary least square (OLS) regression with two machine-learning algorithms that can be applied to regression analysis: stochastic gradient descent (SGD) algorithm and support vector regression (SVR). SGD algorithm, as an iterative approach to optimize the objective function, has been widely employed in statistical estimation for large-scale data due to its computational competence and memory efficiency (Chen et al., 2020). SVR is an application of the support vector machine (SVM), which is well known for its satisfactory performance in binary classification problems. SVR is less popular than SVM, as Awad and Khanna (2015) point out, but has been regarded as an effective tool in real-valued function estimation.
To compare these three regression algorithms, the authors construct a model describing and predicting the determinants of behavioral intentions to tuberculosis (TB) screening. TB is one of the biggest global health threats. Given that TB screening can reduce TB prevalence and mortality rates in the population (Marks et al., 2019), predicting the determinants of TB screening behaviors has long been one of the most important topics in TB-related health communication research (e.g., Hochbaum, 1956; Naidoo & Taylor, 2013; Rosenstock, 1974). Using cross-sectional data collected by the Korea Centers for Disease Control and Prevention (KCDC) to evaluate a national campaign for TB prevention in 2015, this study attempts to compare model performance, predictive performance, optimization technique, and computational speed among the three regression algorithms.
The purpose of this study is not to find which regression method would be best and should be used, but rather to provide an arena to discuss a broader and more practical range of choices for various statistical techniques of regression analysis. The latter leads the authors to recall the famous phrase stated by Box and Draper (1987); “all models are wrong, but some models are useful”. Since every statistical model is calculated based on the observed data, the process underpinning social practices cannot be fully explained (Fox, 2016). As such, a model assumed to operate well in one specific domain may not exhibit satisfactory performance in another domain (Murphy, 2012). In this regard, no statistical model can explain a social phenomenon perfectly. Nevertheless, we should make an effort to seek a better model to explain the social phenomenon, since ‘some models are useful’. Although all models are wrong, an abstraction provided from models can provide several meaningful insights (Enderling & Wolkenhauer, 2021).
OVERVIEW OF THREE REGRESSION ANALYSES
While traditional and ML-based approaches differ in philosophy and purpose, these two approaches have the same roots in that they use a regression model such as Y = αX + β and estimate the best model with the least residuals. However, several differences in terminology between the approaches can cause confusion. For example, the ML-based approach often uses a term that optimizing a loss function rather than estimating regression coefficients. Given that the OLS estimation can be included in the ML-based approach in a broad sense, this study employed terms of the ML-based approach to avoid confusion.
Ordinary Least Square
Basically, the OLS constructs a model as a formula combining predictors and parameters. For example, if there are three predictors, the model function is the same as Equation 1.
| (1) |
where y is the target variable, β’s are predictors, β’s are parameters, and Є is an error term representing the unexplainable population variance with the model. In addition, Equation 1 is generally expressed in a matrix form in Equation 2.
| (2) |
As mentioned above, in the regression problem, the main goal of modeling is minimizing residuals based on a loss function, and the loss function of the OLS method is the residual sum of squares (RSS) in Equation 3.
| (3) |
where n is a sample size, yi is ith target value of data, and is ith predicted value through the model. Then, based on Equation 3, the OLS method calculates the estimator of β that can minimize the RSS through Equation 4.
| (4) |
Even though the OLS method is beneficial in light of that it can estimate parameters based on relatively simple matrices, the OLS method must meet various assumptions, such as normality and homogeneity of variance (see Fox, 2016, p. 126). The estimated parameters are regarded as the best linear unbiased estimator (BLUE) for β only when they satisfy specific statistical assumptions, or otherwise the is no longer reliable. In addition, computing invertible matrices in Equation 4 is another factor to hinder estimation and reduce the reliability of results since not all matrices are invertible matrices.
Stochastic Gradient Descent
The SGD is a variation of the gradient descent (GD) algorithm and utilizes a similar loss function to the OLS method. However, the GD and OLS have a fundamental difference, where the GD updates parameter values gradually by differentiation, namely gradient. Unlike the OLS method, the loss function of GD in a linear regression problem is used the mean squared error (MSE) in Equation 5 to reduce the effect of a sample size. In addition, 1/2 is multiplied by the MSE to offset the differential coefficient.
| (5) |
Under Equation 5, to calculate the minimum MSE value, the GD starts its iteration from a random point and calculates the gradient by using partial derivative with respect to β in Equation 6,
| (6) |
where J(β) is the loss function, and βj is the jth predictor. Through the gradient derived from Equation 6, we can access two pieces of information: direction and approximate distance from the minimum point. Since a gradient of each point gets bigger when the distance between the point and the minimum point gets farther. Furthermore, if a gradient has a positive value, it means that the minimum point is located in the negative direction and vice versa.
Therefore, the loss function can be optimized based on a gradient. As Equation 7, the previous parameter is updated the next parameter by subtracting the gradient of the previous coefficient from .
| (7) |
In Equation 7, we can know that the GD algorithm updates parameters by moving an α distance considering gradient and repeats this process until the loss function computes a small enough value. Therefore, α, usually known as a learning rate, plays a pivotal role in the GD algorithm. If the α is too large, results will alter across a wide range; conversely, if the α is too small, it will take tremendous time to converge. Therefore, determining the adequate learning rate requires a researcher's experience, and various studies have developed effective methods to decide the learning rate (Wu et al., 2018).
Generally, the GD yields reliable results when the learning rate and iteration are set satisfactory, and it has competitive advantages to the OLS method because there is no need to consider inverse matrices computation and statistical assumptions. In this respect, the GD is one of the most popular algorithms used in optimization processes (Ruder, 2016). In order to find the optimal model parameters that minimize the loss function, various optimization algorithms have developed. The SGD has been widely employed as a universal optimization algorithm. The SGD has the same process as the GD, except it estimates parameters based on randomly selected data. Therefore, unlike the GD, the SGD is easy to escape from the local minimum when a loss function is a non-convex form, and it takes less time to optimize (Bottou, 1991).
Support Vector Regression
SVM is well known for its satisfactory performance in various classification problems since it is robust to bias and has no need for statistical assumptions, and guarantees the global minimum (Auria & Moro, 2008). The basic logic of the SVM is calculating a hyperplane that maximizes boundaries between groups of data, and it can solve classification problems not clearly divided in the lower dimension by projecting data in a higher dimension. For example, as Figure 1 illustrates, a non-linear line is required to separate two groups in the two-dimensional space. On the other hand, two groups can be divided by a flat surface when the data is expanded into the three-dimensional space, and the flat surface is called a hyperplane.
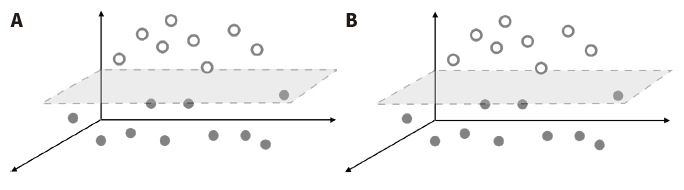
Illustration of Data in Coordinate SpaceNote. Panel A: Data in the two-dimensional space. Panel B: Data in the three-dimensional space.
The optimal hyperplane can be determined by maximizing the distance between two groups, but numerous optimal hyperplanes can exist. To solve this problem, the SVM employs the concept of support vectors. The support vector refers to a set of data with a specific distance from the optimal hyperplane, and there are two support vectors apart from the optimal hyperplane with a c distance. In addition, all data must be divided into the positive or negative hyperplane by the optimal hyperplane following Equation 8.
| (8) |
In most practical situations, the soft margin SVM is typically utilized based on the hard margin SVM in Equation 8 since classifying all data perfectly is sometimes unfeasible due to abnormal data (see Noble, 2006). The soft margin SVM can include data that cannot be classified exactly in two hyperplanes without changing the results by adding a slack variable.
| (9) |
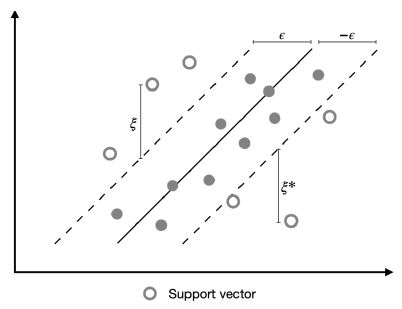
Based on the SVM, the SVR modifies the maximization problem to the minimization problem. In other words, the SVR finds a hyperplane that can capture as many data point as possible. Although many loss functions are available in SVR problems, the є-insensitive function is the most widely utilized.
| (10) |
satisfying the following conditions:
where ||W|| means the Euclidean distance, є is an allowable noise, ξ and ξ* are a distance deviating from є and − є, respectively, and c is the penalty assigned data out from 2є distance. As Equation 10 and Figure 2 suggested, data inside 2є distance are considered zero residual, and data outside 2є distance are penalized the amount of c, and become a support vector.
Given that the SVR penalizes parameters, the SVR has a similarity with the ridge regression. However, the SVR is different from the ridge regression not only that the SVR is a non-parametric approach and the ridge regression is a parametric one, but also that data points inside the ‘є-tube’ cannot affect the final solution; only data points outside of the ‘є-tube’ have their impact. On the contrary, the ridge regression, every data is influential to estimation of parameters (Welling, 2004). In addition, the SVR can be flexible even in non-linear problems by utilizing kernel functions (Auria & Moro, 2008). In a classification problem using the SVM, the kernel function allows separate inseparable data in a low dimension by transforming the data into a higher-dimensional space (Noble, 2006). The kernel function in the SVR enables to find a linear hyperplane in a higher dimension rather than to find a non-linear line in a lower dimension. Another advantage of the kernel function is there are numerous types of kernel functions, such as the linear, radial, and polynomial kernel. To address the effect of different kernel functions, this study chooses two kernel functions, the linear and radial kernel, to explore further the adaptability of the ML-based approach in social science research.
Determinants of Tuberculosis Screening Intention
TB is an airborne infectious disease caused by Mycobacterium tuberculosis, and it is transmitted through cough, sneeze, or talk of a TB patient. Although the new incidence of TB has continued to decline and the Korean government has made an effort to control TB, Korea still has the highest TB incidence rate and second high mortality among OECD countries (World Health Organization, 2021). TB screening can be an effective solution to reduce the incidence of TB. In fact, numerous studies showed that TB screening is one of the good approaches to reduce TB prevalence and mortality rate (e.g., Marks et al., 2019).
This study attempted to explore the determinants of TB screening behavior based on the theoretical framework of the health belief model (HBM). The HBM, as one of the useful explanatory models predicting individuals’ health behavior, has been widely employed to explain the relationship between an individual’s health belief and health behavior since it was first developed in the early 1950s. The HBM posits that two components, such as threat perception and behavioral evaluation, predict individuals’ health-related behavior. Threat perception consists of two belief constructs, such as perceived susceptibility and perceived severity, and behavioral evaluation again consists of two belief constructs: perceived benefits and perceived barriers. The model also includes a cue to action that can trigger health behavior when appropriate beliefs are held. In the late 1980s, self-efficacy was added to the model, which refers to the level of an individual’s confidence in his or her ability to successfully perform a recommended behavior. The model predicts that people will be more likely to be motivated to act if they believe they are susceptible to a negative health outcome (perceived susceptibility), if they perceive the severity of the negative health outcome (perceived severity), if they believe a recommenced behavior leads to other positive outcomes (perceived benefits), and if they perceive few negative attributes related to the health action (perceived barriers) (Abraham & Sheeran, 2005; Rosenstock, 1974). The model also posits that people’s perception of self-efficacy is positively associated with their health actions (Abraham & Sheeran, 2005).
In addition, including two social psychological constructs in the model, such as optimistic bias and social norms, this study also explores their roles in explaining behavioral intention, especially TB screening intention. First, optimistic bias functions as a barrier to health behavior, which weakens individuals' perceived threats such as perceived severity and perceived susceptibility (Weinstein, 1980). Works of literature on optimistic bias posit that people perceive threats through a social comparison process, and they are more likely to underestimate their threats than those of others (Weinstein, 1980).
Second, social norms refer to an opinion, attitude, and pattern of behavior that are authorized by a group and expected to be shared by members of a group (Fisher & Ackerman, 1998). There are two components of social norms; one is the descriptive norm, and the other is the injunctive norm. Based on previous studies, it could be predicted that the more certain actions are perceived as followed by the majority in society, and the more receptive others are to those actions, the higher the individual is likely to perform them (Kim, 2018; Schultz et al., 2007). Given that Korean people are more likely to be affected by social norms to avoid disgraceful consequences (Sohn & Lee, 2012), the authors posit that social norms could be a crucial determinant for TB screening intention.
METHOD
Data
This study utilized the survey data from an evaluation of 2015 TB media campaign effectiveness by KCDC. The survey was designed post-test only and included various questionaries related to TB screening intention such as TB awareness, TB knowledge, HBM variables, and social norms. The research surveyed 1,000 Korean citizens aged from nineteen to sixty-nine, who were selected through multi-stage stratified random sampling by administrative districts, gender, and age. The total response rate was 22.1%, and the sampling error was ±3.1% with a 95% confidence interval. Professionally trained interviewers administered face-to-face interviews from 9th to 23rd November, right after the media campaign was finished.
Of respondents (M = 43.64 years old, SD = 12.50), 508 individuals identified as men (50.8%), and 492 (49.2%) as women. In addition, 516 individuals had high school graduates or a lower level of education (51.6%), and 484 (48.4%) had college graduates or a higher level of education.
Measures
Eleven variables were selected through the survey data as predictors of the TB screening intention model, and all items were measured on a fivepoint scale except TB knowledge, campaign exposure, and demographic variables. The detailed measurement items are available on request from the authors.
Seventeen items were used to measure five dimensions of the HBM: perceived susceptibility, perceived severity, perceived benefit, perceived barrier, and self-efficacy. A confirmatory factor analysis suggested a single-factor solution, so the mean of items of each dimension was computed to create a scale (perceived susceptibility: M = 2.88, SD = .83, r = .59; perceived severity: M = 3.28, SD = .71, McDonald’s ω = .79; perceived benefit: M = 3.80, SD = .59, McDonald’s ω = .69; perceived barriers: M = 3.10, SD = .70, McDonald’s ω = .73; self-efficacy: M = 3.72, SD = .54, McDonald’s ω = .71).
To measure TB knowledge, twenty items from six sections, including the cause of TB, symptoms of TB, TB screening, TB treatment, and TB policy were used. The percentage of correct answers was calculated for each participant to create a total knowledge score (M = 49.56, SD = 19.20), and the maximum score was 100.
Exposure to the campaign was measured by aided recall questions. Respondents who responded 'yes' to one of the recall questions were classified as the exposed group. 34.1% of respondents were exposed to the media campaign, while 65.9% were unexposed.
TB screening intention was measured using three items. A confirmatory factor analysis suggested a single-factor solution, so the mean of items of each dimension was computed to create a scale (M = 3.62, SD = .66, McDonald’s ω = .77).
Data Pre-processing
The entire dataset is separated into the train and test data sets, and each data set contains 80% and 20% of the data, respectively. A 3-fold cross-validation method was employed for ML-based models to select the most stable hyperparameters and ensure the robustness of the model before comparing (Dangeti, 2017) since the performance of ML-based models is susceptible to hyperparameter settings. In addition, data was z-standardized before optimizing to remove the impact measurement units.
Comparison Criteria
This study compared each modeling method in terms of the impact of each predictor, model performance, and computational speed to optimize a train model. First, the impact of each predictor was measured by the relative variance importance (RVI). The RVI is calculated based on the MSE, and if a specific predictor contains significant information, a model including the predictor has a larger MSE than a model without the predictor (Liu & Zhao, 2017). The authors computed the RVI through Equation 11 (see Hadavandi et al., 2017).
| (11) |
where VIi = |MSEfull model − MSEa model except for predictor i|, n is the total number of independent variables, and i is the ith predictor.
Second, the root mean squared error (RMSE), the mean absolute error (MAE), R2, and the correlation between observations and predicted values were used as overall performance. These four measures have typically been employed for regression-based model comparison and demonstrate how well a model explains and predicts data.
Finally, the computational speed of each method is measured by the total elapsed time to optimize the training model.
RESULTS
The analysis was conducted using the R programming language and statistical software version 4.1.0 (R Core Team, 2021). The basic lm function, the gradDescent package (Wijaya et al., 2018), and the e1071 package (Meyer et al., 2021) were utilized to estimate the OLS, the SGD, and the SVR, respectively. The computational speed was measured by the tictoc package (Izrailev, 2021). Prior to optimizing the model, bivariate relationships between the predictors at baseline were examined. There was no evidence to suspect abnormality and multicollinearity. The table of zero-order correlations between the predictors is available on request from the corresponding author.
To begin with, there was a slight violation of the normality assumption, but it was not significant enough to suspect that the OLS estimators were biased. Therefore, the authors conclude that the OLS model satisfied all assumptions, and the OLS model was statistically significant (F[13, 788] = 21.5, p < .001). In ML-based models, the authors selected hyperparameters of each method as α = .001 and 200,000 iterations for the SGD, c = .01, є = .01 for the SVR with the linear kernel (SVRL), and c = 2, є = .01, γ = .01 for the SVR with the radial kernel (SVRR), based on the value of the R2, RMSE and the MSE as a result of 3-fold cross-validation.
Estimated parameter values were calculated in the three linear models, and it can be confirmed that most parameters had similar values (see Table 2). Even though some estimated parameter values had a different sign, there were limited to the only predictors having low parameter values. For example, education level had the negative sign in the OLS and SVRL model (βOLS = -.006, βSVR.Linear = -.016), but the SGD model showed the positive sign (βSGD = .058). Moreover, the age predictor had a similar pattern of result (βOLS = .007, βSGD = .022, βSVR.Linear = -.013). However, all models were optimized with the highest estimated parameter value as the injunctive norm (βOLS = .363, βSGD = .359, βSVR.Linear= .361).
Furthermore, the RVI also demonstrated the similarity and the differences (see Table 2). As the similarity, the injunctive norm was the most important predictor in all models (RVIOLS = .732, RVISGD = .618, RVISVRL = .715, RVISVRR = .402), and overall RVIs of predictors displayed a similar range of values. On the contrary, the RVI of TB knowledge was only notably high in the SVRR (RVIOLS = .060, RVISGD = .014, RVISVRL = .062, RVISVRR = .129). This trend can be visually confirmed by Figure 3.
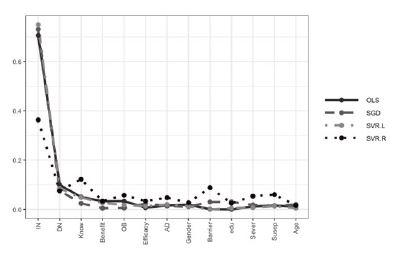
Comparing the RVI of Each Predictor Between Four MethodsNote. SVR.L = SVR with the linear kernel; SVR.R = SVR with the radial kernel; IN = injunctive norm; DN = descriptive norm; Know = TB knowledge; OB = Optimistic bias; Benefit = perceived benefit; Susep = Perceived susceptibility; AD = TB campaign exposure; Barrier = perceived barrier; Efficacy = self-efficacy; edu = education level.
As demonstrated in Table 3, the model that took the least elapsed time to optimize model was the OLS, and it took about .01 seconds for model training. Next, it was followed by the SVRL (.11 seconds), SVRR (.12 seconds), and SGD (7.64 seconds). In terms of the model performance measures, there was no significant difference except SVR with the radial kernel. The average model performance of three train models without the SVRR model was as follows: R2 = .252, r = .507, MAE = .673, RMSE = .861. The SVRR model yielded the highest R2 (.335) and r (.582), while having the lowest MAE (.620) and RMSE (.815). This result was the same in the test model; even though performance measures were decreased in all models, the SVRR model displayed the best performance among the four models (R2 = .209, r = .458, MAE = .667, RMSE = .888). However, when comparing the train and test model, the model performance measures of SVRR model decreased the most.
DISCUSSION
Social science researchers have inevitably relied on data analysis methods to understand and explain complex social phenomena. Numerous statistical methods have been developed and employed, and in particular, regression analysis has long been gained favor with social science researchers. The ML-based approach to regression analysis has been attracting attention as a new analytical method in the field of social science. In order to explore the utilities of ML-based regression analysis in the area of communication research, this study attempted to compare OLS regression with two popular machine-learning algorithms such as SGD algorithm and SVR in terms of model performance, the impact of each predictor, optimization technique, and computational speed. To compare these three regression algorithms, this study constructed and analyzed a model predicting the determinants of behavioral intentions to TB screening. Based on the results, the following issues can be discussed.
Is the ML-based Approach a Useful Tool for Communication Researchers?
This study found no clear evidence of superior performance of the ML based approach, and the findings are not quite different from the result of a recent review (Christodoulou et al., 2019) comparing ML models with traditional regression models. In terms of RVI, the injunctive norm was the most important predictor in all four models even though the RVI of TB knowledge was notably high in the SVRR model compared to those of other models. It is found that, however, the RVI of TB knowledge was only notably high in the SVRR compared other models.
In spite of the findings of this study, however, it should be cautious to assert that the ML-based approach to regression analysis is not useful compared to the traditional OLS. Like other statistical methods for frequentists, performing regression analysis is also based on strong statistical assumptions, namely assumptions about the data-generating process. We have learned that one of the advantages of OLS is that its coefficient estimates are unbiased if the assumptions are fully satisfied, which are seldom satisfied in practice. As Velleman and Welsch (1981, p. 234) note, “multiple regression analyses can be severely and adversely affected by failures of the data to adhere to the assumptions that customarily accompany regression models.”
The ML-based approach is relatively free from assumptions about the data-generating process. It makes only minimal assumptions that data are drawn independently and identically distributed from an unknown distribution (Buskirk et al., 2018; Rudin, 2015). Although no serious assumption violations were found in this study, it is very rare to find that all assumptions are fully satisfied in practice. Given that data analysis practices in which testing and reporting of assumptions are often ignored in most social science research, the ML-based approach may be a good alternative to OLS in that it fully captures the features of the data and make a data-driven description even when statistical assumptions are violated. For example, the SVRR model showed much higher importance of the TB knowledge predictor compared to the other models, which could be interpreted as a result that the nonlinearity of the SVRR model learned more freely about features of data. This can be exceptionally useful for exploratory studies, which do not have enough prior information or background knowledge about the data-generating process.
Addressing the difference in scientific philosophies between deductive research and inductive research can be another good point for discussing whether the ML-based approach is a useful tool for communication researchers. Both inductive research (theory-building) and deductive research (theory-testing) are essential for the progress of science and are closely intertwined, but the purposes of building a statistical model between these two camps differ depending on whether the researcher’s main concern is to explain or predict social phenomena.
Although all statistical models are fundamentally employed to provide descriptions of the associations among one or more operational variables, their roles are distinguished into two different research purposes, namely explanation and prediction (Flora, 2017). While an explanatory model is to explore association among observed variables or test hypotheses related to the underlying theory from a given data set, a predictive model is to predict the outcome of interest applicable to new cases that have not yet been observed. In the context of this study, for example, the explanatory models are built to explain the association between TB knowledge and TB screening behavior in a population is, whereas the predictive models are built to predict what an individual’s TB screening behavior will be like given the individual’s TB knowledge score.
Researchers in traditional research tend to focus more on explanatory models rather than predictive models although these two types of modeling are rarely distinguished in real research practices. However, no one would deny that prediction is an important goal of science, just as no one would argue that explanation should not be the goal of science. More precise the prediction, the better the theory (Shoemaker et al., 2004). Nevertheless, it is true that there are statistical and pragmatic tension between explanation and prediction, even the role and importance of prediction have long been overlooked in traditional social science research (Buskirk et al., 2018; Hindman, 2015; Yarkoni & Westfall, 2017). While explanatory models focus on estimating (the parameter of the model), prediction models focus on predicting (the prediction of the outcome).
From the perspective of prediction, the serious weaknesses of OLS can result from the wrong practices that can be easily found in many areas of social science. The practice of shotgun approach (Kerlinger & Pedhazur, 1973) or pet variable (Hindman, 2015), which pejoratively refers to the practice of throwing all possible predictors into the regression model to find whether their chosen predictor is statistically significant after controlling for a bunch of other things, can severely impair the reliability of regression coefficients and further make the replication of research results more difficult. The parameter estimated with the sample data at hand can no longer be a good parameter in out-of-sample data. This problem occurs more seriously in high-dimensional data and leads to overfitting of the model. In this situation, estimating the regression weights and testing their statistical significance might be useless for the model generalization. Rather, it could be more meaningful for researchers to show how many predictions actually improves by adding specific variables to the model. We are well aware, as Yarkoni and Westfall (2017) pointed out, that rejecting hypotheses is not a primary goal of the research. Given that ML-based techniques (e.g., K-fold cross-validation, regularization, hyperparameter search, and automatic feature engineering) can reduce the out-of-sample error and produce more stable findings across different research, the ML-based approach can be better alternatives to OLS. For instance, the K-fold cross validation employed in this study is more robust to overfitting, allowing researchers to better estimate the out-of-sample predictive performance of the model.
Finally, the ML-based approach has the potential for broadening the prospect of communication research by combining it with big data. Recent advances in data handling techniques have made it easy for communication researchers to obtain a wider range of behavioral data that naturally occurs through digital technologies, such as social media, smartphones, and wearable devices; the volume and complexity of these behavior-related big data are increasing exponentially. As mentioned earlier, the ML-based approach can be beneficial in capturing the hidden structure of data since it is a data-driven algorithm. It should be noted, however, that this does not mean that the traditional simple approaches (e.g., OLS or logistic regression) cannot be utilized in analyzing big data, especially high-dimensional data. Although as the size and complexity of data increase, the ML-based approach may have utilities in terms of both computational efficacy and statistical limitations (e.g., multicollinearity or heteroscedasticity, see Fan et al., 2014), there is no solid evidence to prove the superiority of ML-based approaches over traditional statistical approaches in terms of big data analysis (Christodoulou et al., 2019). Nevertheless, regarding compatibility with big data, ML algorithms have the advantage of being able to leverage different types of data, such as images, videos, voices, natural languages, or even sensor data. Given that social science researchers have faced the realistic challenges of having to analyze a variety of naturally generated behavioral data beyond the data from typical traditional sources (e.g., survey or experiment), the benefit gained from the use of ML algorithms is obvious.
Is the ML-based Approach a Panacea for Communication Researchers?
The evolution of ML algorithms seems to promise a rosy future in almost every research domain, and social science is no exception. The SVRR model demonstrated the best performance measures in this study, but it is still questionable that the ML-based approach guarantees the best model compared to the traditional approach in terms of overfitting and the black-box model. Based on the findings in this study, two critical problems of the ML-based approaches can be discussed as follows.
First, the ML-based approach is not free from statistical overfitting even though it prevents procedural overfitting compared to the OLS. Given that the overfitting is related to the bias-variance tradeoff, it occurs when an optimizing process contains excessive variance compared to bias (Briscoe & Feldman, 2011). The overfitting problem of the ML-based approach is mainly caused by the fact that it has more freedom in the optimizing process. As could be confirmed in this study, the results that the signs of parameter values were calculated differently to the model, and the largest performance gap between the train and test model of SVRR can be interpreted as the tendency of overfitting.
Second, the ML-based approach sometimes produces uninterpretable results. The ML-based models have often been criticized as ‘black boxes’ since understanding their internal procedure is unfeasible (Radford & Joseph, 2020). Although there have been a lot of efforts to establish interpretable ML models, this seems to require further efforts and additional processes. In fact, ML-based models employed in this study did not offer as much information as the OLS model; there were no null hypothesis significance testing (NHST) results of individual predictors, and even the SVRR model could not compute individual parameter values. Given that, it is questionable that the ML-based approach is suitable for a situation that is essential to explain the relationship between predictors. Nevertheless, the low interpretability of a black-box model cannot always reduce its utility in communication research. For instance, causal inference, as Kleinberg and colleagues (2015) claimed, cannot be a central aspect of some problems in policymaking, and empirical policy focusing on prediction can generate a large social impact. Also, the prediction-focused attribute of the ML-based approach can be exceptionally beneficial in practical and urgent situations such as the COVID-19 pandemic. For example, various ML-based approaches have been used to explore public perceptions of COVID-19 vaccination on social media and predict its future intention; spatiotemporal sentiment analysis (Hu et al., 2021), two-stage clustering (Hashimoto et al., 2021), topic modeling (Gokhale, 2020), semantic network analysis (Luo et al., 2021).
Third, it should be noted that there is no single machine learning algorithm that performs universally best for all problems. Theoretically, the best algorithm for a particular problem may exist only if it is specific to the particular problem under consideration. As so-called No Free Lunch theorems (NFL theorems) insisted, “if an algorithm performs well on a certain class of problems, then it necessarily pays for that with degraded performance on the set of all remaining problems” (Wolpert & Macready, 1997, p. 69). Thus, the results of model comparisons in this study could be limited to a specific type of theoretical model, the so-called HBM, or the data used. According to the NFL theorems, many standard learning algorithms as a data-driven approach must inherently have a certain bias, and they are model-dependent (for more review, see Sterkenburg & Grünwald, 2021). Therefore, it is important that the theoretical or conceptual model in which the ML algorithm is used should be well-defined and that the algorithm optimized for it should be applied.
In fact, the model performance can vary depending on the optimization algorithms, such as hyperparameter tuning, advanced optimization techniques, or feature selection/extraction processes. For example, the results of this study showed that SGD had the slowest computational speed among the four models. These results might be due to frequent updates of the SGD. It is true that the SGD has a fundamental limitation due to frequent that are computationally expensive updates. As SGD is updated more frequently, the loss function may have severe oscillations affecting convergence. Although selecting the proper learning rate is crucial in the SGD algorithm (Ruder, 2016), but choosing a proper learning rate can be difficult, and sometimes applying the same learning rate to all parameter might be inappropriate. To solve this limitation, various optimization techniques based on the SGD algorithm have been developed, such as momentum method, Adagrad (adaptive subgradient) method, RMSProp (root mean square prop) method, and Adam method, etc (see Ruder, 2016).
In final, measurement error must be a major challenge in developing useful machine learning algorithms (Jiang et al., 2020). Several studies showed that measurement error (referred to as label noise in the area of ML) could affect the overall performance of ML algorithms. For example, measurement error could lead to severely underfitting the true relationships (Jacobucci & Grimm, 2020), to inaccurate predictor selection (Frénay & Verleysen, 2013), and to decrease prediction performance (Nettleton et al., 2010). Nevertheless, it is true that the validity and reliability of measurement models and their impacts on the results derived have received little attention in the field of machine learning. Further research should be needed to examine how measurement error affects various ML algorithms and to develop ML algorithms to verify the validity and reliability of measurement model.
CONCLUSION
The authors’ short and decisive answer to the main question of this study, Is the ML-based approach a useful tool for communication researchers?, is Could be. Machine learning is not magic. Machine learning, Grimmer and colleagues (2021) noted, is just tools, not new magic methods to resolve the long-standing problems facing social scientists. Perhaps the hybrid approach is the smartest idea in the use of these two approaches. As discussed above, the traditional approach is representative of a deductive, top-down, or theory-driven approach; on the contrary, the ML-based approach represents an inductive, bottom-up, or data-driven approach. These different philosophical and methodological attributes can make researchers consider these two approaches as a competitive relationship, but they are complementary to each other (see Chen et al., 2018; Grimmer, 2015; Radford & Joseph, 2020). As Yarkoni and Westfall (2017) noted, since a short-term focus on prediction can ultimately improve researchers’ ability to explain the causes of behavior in the long term, an emphasis on prediction should be viewed not as an opponent of explanation but rather as a complementary goal that can ultimately increase theoretical understanding. Finally, the authors would like to conclude by restating Stephen Jay Gould’s comment (Gould, 1988): Popular misunderstanding of science and its history centers upon the vexatious notion of scientific progress - a concept embraced by all practitioners and boosters, but assailed, or at least mistrusted, by those suspicious of science and its power to improve our lives. The enemy of resolution, here as nearly always, is that old devil Dichotomy (p. 16).
Acknowledgments
This article is based on the MA thesis completed by Dayeoun Jang (2021), and this work was supported by the research fund of Hanyang University (HY-2019-G).
References
- Abraham, C., & Sheeran, P. (2005). The health belief model. In M. Conner & P. Norman (Eds.), Predicting health behaviour: Research and practice with social cognition models (2nd ed., pp. 30−69). Open University Press.
-
Auria, L., & Moro, R. A. (2008). Support vector machines (SVM) as a technique for solvency analysis. DIW Berlin Discussion Papers, 811. 1−16.
[https://doi.org/10.2139/ssrn.1424949]

-
Awad, M., & Khanna, R. (2015). Support vector regression. In M. Awad & R. Khanna (Eds.), Efficient learning machines: Theories, concepts, and applications for engineers and system designers (pp. 67−80). Apress.
[https://doi.org/10.1007/978-1-4302-5990-9_4]

- Bottou, L. (1991). Stochastic gradient learning in neural networks. Proceedings of Neuro-Nımes, 91(8), 1−12. http://leon.bottou.org/publications/pdf/nimes-1991.pdf
- Box, G. E. P., & Draper, N. R. (1987). Empirical model-building and response surfaces. Wiley.
-
Breiman, L. (2001). Statistical modeling: The two cultures (with comments and a rejoinder by the author). Statistical Science, 16(3), 199−231.
[https://doi.org/10.1214/ss/1009213726]

-
Briscoe, E., & Feldman, J. (2011). Conceptual complexity and the bias/variance tradeoff. Cognition, 118(1), 2−16.
[https://doi.org/10.1016/j.cognition.2010.10.004]

-
Buskirk, T. D., Kirchner, A., Eck, A., & Signorino, C. S. (2018). An introduction to machine learning methods for survey researchers. Survey Practice, 11(1), 1−10.
[https://doi.org/10.29115/SP-2018-0004]

-
Chen, N.-C., Drouhard, M., Kocielnik, R., Suh, J., & Aragon, C. R. (2018). Using machine learning to support qualitative coding in social science: Shifting the focus to ambiguity. ACM Transactions on Interactive Intelligent Systems, 8(2), 1−20.
[https://doi.org/10.1145/3185515]

-
Chen, X., Lee, J. D., Tong, X. T., & Zhang, Y. (2020). Statistical inference for model parameters in stochastic gradient descent. Annals of Statistics, 48(1), 251−273.
[https://doi.org/10.1214/18-AOS1801]

-
Christodoulou, E., Ma, J., Collins, G. S., Steyerberg, E. W., Verbakel, J. Y., & Van Calster, B. (2019). A systematic review shows no performance benefit of machine learning over logistic regression for clinical prediction models. Journal of Clinical Epidemiology, 110, 12−22.
[https://doi.org/10.1016/j.jclinepi.2019.02.004]

- Dangeti, P. (2017). Statistics for machine learning: Techniques for exploring supervised, unsupervised, and reinforcement learning models with Python and R. Packt Publishing.
-
Enderling, H., & Wolkenhauer, O. (2021). Are all models wrong? Computational and Systems Oncology, 1(1), e1008.
[https://doi.org/10.1002/cso2.1008]

-
Ethington, C. A., Thomas, S. L., & Pike, G. R. (2002). Back to the basics: Regression as it should be. In J. C. Smart & W. G. Tierney (Eds.), Higher education: Handbook of theory and research (pp. 263−293). Springer.
[https://doi.org/10.1007/978-94-010-0245-5_6]

-
Fan, J., Han, F., & Liu, H. (2014). Challenges of big data analysis. National Science Review, 1(2), 293−314.
[https://doi.org/10.1093/nsr/nwt032]

-
Fisher, R. J., & Ackerman, D. (1998). The effects of recognition and group need on volunteerism: A social norm perspective. Journal of Consumer Research, 25(3), 262−275.
[https://doi.org/10.1086/209538]

- Flora, D. B. (2017). Statistical methods for the social and behavioural sciences: A model-based approach. SAGE Publications.
-
Fox, J. (1991). Regression diagnostics: An introduction. SAGE Publications.
[https://doi.org/10.4135/9781412985604]

- Fox, J. (2015). Applied regression analysis and generalized linear models (3rd ed.). SAGE Publications.
-
Frénay, B., & Verleysen, M. (2014). Classification in the presence of label noise: A survey. IEEE Transactions on Neural Networks and Learning Systems, 25(5), 845−869.
[https://doi.org/10.1109/TNNLS.2013.2292894]

-
Galton, F. (1886). Regression towards mediocrity in hereditary stature. The Journal of the Anthropological Institute of Great Britain and Ireland, 15, 246−263.
[https://doi.org/10.2307/2841583]

-
Gokhale, S. S. (2020). Monitoring the perception of Covid-19 vaccine using topic models. 2020 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing , Sustainable Computing & Communications, Social Computing & Networking, 867−874.
[https://doi.org/10.1109/ISPA-BDCloud-SocialCom-SustainCom51426.2020.00134]

- Gould, S. J. (1988). Pretty pebbles: Despite wicked curves, detours, and delays, the rocky road toward scientific truth is a great trip. Natural History, 97(4), 14−25. https://digitallibrary.amnh.org/handle/2246/6494
-
Grimmer, J. (2015). We are all social scientists now: How big data, machine learning, and causal inference work together. Political Science & Politics, 48(1), 80−83.
[https://doi.org/10.1017/S1049096514001784]

-
Grimmer, J., Roberts, M. E., & Stewart, B. M. (2021). Machine learning for social science: An agnostic approach. Annual Review of Political Science, 24, 395−419.
[https://doi.org/10.1146/annurev-polisci-053119-015921]

-
Hadavandi, E., Hower, J. C., & Chelgani, S. C. (2017). Modeling of gross calorific value based on coal properties by support vector regression method. Modeling Earth Systems and Environment, 3(1), 1−7.
[https://doi.org/10.1007/s40808-017-0270-7]

-
Hashimoto, T., Uno, T., Takedomi, Y., Shepard, D., Toyoda, M., Yoshinaga, N., Kitsuregawa, M., & Kobayashi, R. (2021). Two-stage clustering method for discovering people’s perceptions: A case study of the COVID-19 vaccine from twitter. 2021 IEEE International Conference on Big Data (Big Data), 614−621.
[https://doi.org/10.1109/BigData52589.2021.9671982]

- Hayes, A. F. (2005). Statistical methods for communication science. Routledge.
-
Hindman, M. (2015). Building better models: Prediction, replication, and machine learning in the social sciences. The ANNALS of the American Academy of Political and Social Science, 659(1), 48−62.
[https://doi.org/10.1177/0002716215570279]

-
Hochbaum, G. M. (1956). Why people seek diagnostic X-rays. Public Health Reports, 71(4), 377−380.
[https://doi.org/10.2307/4589418]

-
Hu, T., Wang, S., Luo, W., Zhang, M., Huang, X., Yan, Y., Liu, R., Ly, K., Kacker, V., She, B., & Li, Z. (2021). Revealing public opinion towards COVID-19 vaccines with Twitter data in the United States: Spatiotemporal perspective. Journal of Medical Internet Research, 23(9), e30854.
[https://doi.org/10.2196/30854]

- Izrailev, S. (2021). tictoc: Functions for timing R scripts, as well as implementations of stack and list structures. https://cran.r-project.org/web/packages/tictoc/index.html
-
Jacobucci, R., & Grimm, K. J. (2020). Machine learning and psychological research: The unexplored effect of measurement. Perspectives on Psychological Science, 15(3), 809−816.
[https://doi.org/10.1177/1745691620902467]

- Jang, D. (2021). A comparative study of ordinary least square, Bayesian regression, stochastic gradient descent, and support vector regression for predicting the effects of lifestyle on mobile advertising effectiveness [Unpublished master’s thesis]. Hanyang University.
-
Jiang, T., Gradus, J. L., & Rosellini, A. J. (2020). Supervised machine learning: A brief primer. Behavior Therapy, 51(5), 675−687.
[https://doi.org/10.1016/j.beth.2020.05.002]

- Kerlinger, F. N., & Pedhazur, E. J. (1973). Multiple regression in behavioral research. Holt, Rinehart & Winston.
-
Kim, S.-Y. (2018). Role norm appeal in deterring student binge drinking in the U.S. and South Korea. Asian Communication Research, 15(1), 49−74.
[https://doi.org/10.20879/acr.2018.15.1.49]

-
Kleinberg, J., Ludwig, J., Mullainathan, S., & Obermeyer, Z. (2015). Prediction policy problems. American Economic Review, 105(5), 491−495.
[https://doi.org/10.1257/aer.p20151023]

-
Liu, Y., & Zhao, H. (2017). Variable importance-weighted random forests. Quantitative Biology, 5(4), 338−351.
[https://doi.org/10.1007/s40484-017-0121-6]

-
Luo, C., Chen, A., Cui, B., & Liao, W. (2021). Exploring public perceptions of the COVID-19 vaccine online from a cultural perspective: Semantic network analysis of two social media platforms in the United States and China. Telematics and Informatics, 65, 101712.
[https://doi.org/10.1016/j.tele.2021.101712]

-
Lynch, S. M. (2013). Using statistics in social research: A concise approach. Springer.
[https://doi.org/10.1007/978-1-4614-8573-5]

-
Marks, G. B., Nguyen, N. V., Nguyen, P. T. B., Nguyen, T.-A., Nguyen, H. B., Tran, K. H., Nguyen, S. V., Luu, K. B., Tran, D. T. T., Vo, Q. T. N., Le, O. T. T., Nguyen, Y. H., Do, V. Q., Mason, P. H., Nguyen, V.-A. T., Ho, J., Sintchenko, V., Nguyen, L. N., Britton, W. J., & Fox, G. J. (2019). Community-wide screening for tuberculosis in a high-prevalence setting. New England Journal of Medicine, 381(14), 1347−1357.
[https://doi.org/10.1056/NEJMoa1902129]

- Meyer, D., Dimitriadou, E., Hornik, K., Weingessel, A., & Leisch, F. (2021). e1071: Misc functions of the department of statistics, probability theory group (Formerly: E1071). https://cran.r-project.org/web/packages/e1071/index.html
- Murphy, K. P. (2012). Machine learning : A probabilistic perspective. The MIT press.
-
Naidoo, S., & Taylor, M. (2013). Association between South African high-school learners’ knowledge about tuberculosis and their intention to seek healthcare. Global Health Action, 6(1), 1−8.
[https://doi.org/10.3402/gha.v6i0.21699]

-
Nettleton, D. F., Orriols-Puig, A., & Fornells, A. (2010). A study of the effect of different types of noise on the precision of supervised learning techniques. Artificial Intelligence Review, 33(4), 275−306.
[https://doi.org/10.1007/s10462-010-9156-z]

-
Niu, W.-J., Feng, Z.-K., Feng, B.-F., Min, Y.-W., Cheng, C.-T., & Zhou, J.-Z. (2019). Comparison of multiple linear regression, artificial neural network, extreme learning machine, and support vector machine in deriving operation rule of hydropower reservoir. Water, 11(1), 1−17.
[https://doi.org/10.3390/w11010088]

-
Noble, W. S. (2006). What is a support vector machine? Nature Biotechnology, 24(12), 1565−1567.
[https://doi.org/10.1038/nbt1206-1565]

- R Core Team. (2021). R : A language and environment for statistical computing. https://www.R-project.org/
-
Radford, J., & Joseph, K. (2020). Theory in, theory out: The uses of social theory in machine learning for social science. Frontiers in Big Data, 3, Article 18.
[https://doi.org/10.3389/fdata.2020.00018]

-
Rosenstock, I. M. (1974). Historical origins of the health belief model. Health Education Monographs, 2(4), 328−335.
[https://doi.org/10.1177/109019817400200403]

- Ruder, S. (2016). An overview of gradient descent optimization algorithms. arXiv.
- Rudin, C. (2015). Can machine learning be useful for social science? The Cities Papers: An essay collection from The Decent City initiative. http://citiespapers.ssrc.org/can-machine-learning-be-useful-for-social-science/
-
Schultz, P. W., Nolan, J. M., Cialdini, R. B., Goldstein, N. J., & Griskevicius, V. (2007). The constructive, destructive, and reconstructive power of social norms. Psychological Science, 18(5), 429−434.
[https://doi.org/10.1111/j.1467-9280.2007.01917.x]

-
Shoemaker, P. J., Tankard, J. W., & Lasorsa, D. L. (2003). How to build social science theories. SAGE Publications.
[https://doi.org/10.4135/9781412990110]

- Sohn, Y., & Lee, B. (2012). An efficacy of social cognitive behavior model based on the theory of planned behavior : A meta-analytic review. Korean Journal of Journalism & Communication Studies, 56(6), 127−161.
-
Sterkenburg, T. F., & Grünwald, P. D. (2021). The no-free-lunch theorems of supervised learning. Synthese, 199, 9979−10015.
[https://doi.org/10.1007/s11229-021-03233-1]

-
Velleman, P. F., & Welsch, R. E. (1981). Efficient computing of regression diagnostics. The American Statistician, 35(4), 234−242.
[https://doi.org/10.1080/00031305.1981.10479362]

-
Weinstein, N. D. (1980). Unrealistic optimism about future life events. Journal of Personality & Social Psychology, 39(5), 806−820.
[https://doi.org/10.1037/0022-3514.39.5.806]

- Welling, M. (2004). Support vector regression. Department of Computer Science, University of Toronto. http://www.carc.unm.edu/~andriese/doc/ref2_svr.pdf
- Wijaya, G. P., Handian, D., Nasrulloh, I. F., Riza, L. S., Megasari, R., & Junaeti, E. (2018). gradDescent: Gradient descent for regression tasks. http://cran.nexr.com/web/packages/gradDescent/index.html
-
Wolpert, D. H., & Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1), 67−82.
[https://doi.org/10.1109/4235.585893]

- World Health Organization. (2021). Global tuberculosis report 2021 (Licence: CC BY-NC-SA 3.0 IGO). https://www.who.int/publications/i/item/9789240037021
- Wu, X., Ward, R., & Bottou, L. (2018). WNGrad: Learn the learning rate in gradient descent. arXiv.
-
Yarkoni, T., & Westfall, J. (2017). Choosing prediction over explanation in psychology: Lessons from machine learning. Perspectives on Psychological Science, 12(6), 1100−1122.
[https://doi.org/10.1177/1745691617693393]