Detective Activity Comparing Frequentist (NHST) and Bayesian Methods: Introducing Bayesian Concepts to Students of Communication

Despite the growing popularity of Bayesian approaches to social science, students of communication tend to receive statistical training mostly within the discipline of null hypothesis significance testing (NHST) and therefore remain largely unexposed to the process, utility, and potential applications of Bayesian modeling. Focus on the NHST paradigm is understandable given the main goal of positivists is to reach the truth by continuously ‘winnowing out’ inferior theories rather than continually refining one (see Popper, 1959). Nonetheless, NHST is still limited in its capacity to help achieve such a goal in that it compares an ‘alternative’ hypothesis with a nill null rather than putting multiple theories into competition (see Kim, 2017), which Bayesian analysis incorporates.

Gaining Balance in Quantitative Methods Education

This article proposes that we as communication educators instate a balance in the course curriculum by introducing at least some fundamentals of Bayesian approaches in predominantly NHST-focused quantitative methods courses. At least two considerations justify the proposal. First, with the increasing demand for inter- and cross-disciplinary research, the realm of communication research is rapidly spreading. For instance, discourse analysis is now being automated, and many text analysis techniques employ Bayesian approaches (e.g., naïve Bayes classifier, Latent Dirichlet Allocation [LDA] based topic modeling; see Grimmer & Stewart [2013] for a comprehensive review). While the outcome of automated text analysis may currently remain less sophisticated than those from manual coding, it should be noted that the major purpose of, for example, LDA topic modeling is ‘mining’ insights from text data rather than testing any particular theories. What should be also recalled is that, especially in online environment, enormous amounts of text data are being automatically collected every second, and analyzing them is far beyond human capacity. Students with an exposure to at least some basics of Bayesian approaches will be better equipped with the relevant skillsets needed to survive this new data environment.

Second, as noted above, Bayesian modeling better approximates the manner in which we advance our understanding of human conditions. Unlike NHST, which only assesses the probability of the data given the true null (p[D|H₀]) and provides little information about the theory under investigation (H₁), Bayesian analysis presents the probability of the theory conditional on the data (p[H₁|D]). To the extent that this is how empirical knowledge progresses—that is, continuously updating the theory based on newer observations—the Bayesian approach could be considered a methodological tool that better matches the current practices of scientific research.

Following this line of reasoning, this paper presents a new in-class activity whereby students can learn the basic mechanism of Bayesian analysis, how it differs from NHST, and the methodological implications of both approaches. This initiative is one of the first attempts highlighting NHST and Bayesian analysis in a way that students with little statistical background can fully comprehend. The proposed in-class activity purports to help students ‘experience’ the major limitations of NHST and the Bayesian approach’s potential as a viable alternative (Mueller et al., 2019). In what follows, we (a) discuss major issues of NHST and the Bayesian approach in comparison, (b) introduce the details of the activity, (c) present class debriefing topics, (d) offer an appraisal of feedback from students who participated in the activity, and finally (e) provide recommended adaptations for online/hybrid courses. Hopefully, the current activity could help student participants to develop interest in learning more about Bayesian modeling and machine learning in the future.

Comparing NHST and Bayesian Modeling

While the NHST procedure may be ubiquitous in social scientific communication research courses and is technically correct, we highlight various limitations with this approach. First, the method does not provide information about what the researcher really wants to know, which is the probability for the theory to be true conditional on the data (i.e., p[H₁|D]). Instead, NHST only presents the probability for the immediate data to occur assuming a true null (i.e., p[D|H₀]), which is hardly how the process of learning occurs in reality (see Levine et al., 2008). Second, NHST rarely considers prior knowledge from past research. NHST operates under a pretense that the researcher has no, or little, prior information to quantify the predictions even when past data exist. Finally, NHST minimally corresponds to how scientific theory advances, which requires incessant, incremental updates by constantly incorporating newer data into the model. This disallows a direct examination of the theory (i.e., p[H₁]) and hence precludes the chance to update it. Taken together, the above characteristics are key reasons NHST is considered less than optimal for facilitating the progression of scientific knowledge about human behavior (see Davis et al., 2019).

Among many additional limitations of NHST discussed by social scientists (see Anderson et al., 2000; Boster, 2002; Cohen, 1990; Levine et al., 2008), a final, and the most major, limitation is that NHST relies on an arbitrary rule, the so called “p-value.” A p-value denotes the conditional probability of the data assuming the null is true (i.e., p[D|H₀]). The application of a p-value leads to a dichotomous conclusion around the null rather than the target theory; students are trained to reject the null when p < .05, indicating the probability for the data to be observed is adequately unlikely assuming the null was true. The null is reserved as a possibility when the analysis results in p > .05 (see Kim, 2017). Thus, the p-value limits a researcher’s attention and interpretation of the findings to dichotomous significant or non-significant conclusions, affording less attention to the research hypothesis (Boster, 2002).

On the other hand, scholars praise Bayesian analysis for its capacity to remedy the limitations of NHST (e.g., Anderson et al., 2000; O’Connor, 2017). Bayesian analysis differs from NHST and better aligns with how scientific theory evolves in that it synthesizes prior knowledge from past studies with the immediate data to directly estimate the probability of the research hypothesis conditional on all the data observed (i.e., posterior or p[H₁|D]). This same procedure can be used to update the posterior when newer data become available, which more closely resembles how our understanding of the human condition continually improves as new observations accrue (see Davis et al., 2019).

Efforts have been made to introduce the Bayesian approach to students of social science. The primary focus of most past studies, however, has been to introduce various class activities solely dedicated to teaching Bayes statistics within the discipline, not in comparison with NHST (e.g., Bárcena et al., 2019; Eadie et al., 2019; Hu, 2020; Ruscio, 2003; Sedlmeier & Gigerenzer, 2001; van Doorn et al., 2020). There exist a handful of manuscripts intended to delineate the statistical procedures that NHST and the Bayesian approaches take to reach conclusions and estimate the effect sizes (e.g., Pek & Van Zandt, 2020; Westera, 2021). Few, however, have attempted to develop an in-class activity for students to “experience” the difference between the two traditions and to better understand their philosophical implications in one session.

This paper provides a critical argument and classroom activity to explain and teach the theoretical and methodological assumptions and implications of both NHST and Bayesian analysis. In essence, the argument and activity demonstrate which of the two methods better represents the way in which a scientific theory advances, thereby building upon and extending the previous works and ultimately positioning the paper as a crucial “first-read” for educators in communication wanting to teach their students about the theory and process of Bayesian modeling.

Intended Lessons

The following activity is intended to illustrate the major differences between NHST and Bayesian methods. The activity requires students to assess a fictitious suspect’s guilt using both NHST and Bayesian approaches. At the completion of the current activity, students should understand (a) NHST tells the probability about the data assuming the null is true (i.e., p[D|H₀]), (b) Bayesian analysis informs the probability of the prediction given the data (i.e., p[H₁|D] or a posterior) and allows for updating it by incorporating newer data later, and (c) the Bayesian approach, compared to NHST, corresponds more closely to the way in which empirical knowledge progresses in science.

Description of Activity

This activity can be completed within two, 75-minute class sessions. In the first class session, instructors should provide students with an overview of NHST, or p(D|H₀), and Bayesian modeling, or p(H₁|D). To ensure students have a sufficient theoretical understanding, we provide instructors with two brief descriptions of NHST and Bayesian analysis to guide the first class session. However, instructors should review the entire activity prior to the first class session to identify what information will best suit the needs of their students. In the second class session, instructors should facilitate the class activity and lead a debriefing discussion.

First Session: NHST and Bayesian Modeling Overview

Instructors should prepare as they would for giving a traditional lecture; this might include having access to a whiteboard and whiteboard markers, a laptop/desktop, and a screen projector, or providing students with instructor-developed review materials. Students should be prepared with a writing utensil and a note-taking device. Instructors are recommended to fully review the relevant course contents with the students before the activity.

NHST. The instructor should explain to students that studies adopting the NHST tradition are designed to either falsify (i.e., reject) or support (i.e., fail to reject) a null hypothesis. Additionally, explain that NHST scholars analyze the probabilities of observed data based on the assumption of a true null, or p(D|H₀). Discuss what it means for a finding to be statistically significant or not in terms of confidence level (α) and p-value.

Bayesian analysis. The instructor should then explain that when using Bayesian methods, the aim of the researcher is to assess the credibility of multiple hypotheses based on the observed data, or p(H₁, H₂, ... H_k|D). In this approach, the researcher is not comparing the observed data to a preset null. Instead, the instructor should explain that a Bayesian analysis begins by creating a prior distribution, which shows the respective probability of proposed hypotheses based on scholarly and/or subjective beliefs about a phenomenon. Next, the researcher collects a dataset and mathematically synthesizes it with the prior to produce a posterior, a redistributed credibility of each hypothesis. Importantly, inform students that the posterior can then be used as a new prior for the next test of the event.

Second Session: The Activity

The activity is broken into two components: an NHST activity and Bayesian activity. Prior to starting either activity, the instructor should be prepared with copies of the Evidence Statements (ESs; see Appendix). The instructor should divide the class into small groups of four to five students. Students should be prepared with a writing utensil, a note-taking device, and a calculator. To begin and set the groundwork for both activities, the instructor should pass out a copy of the ESs to each team and offer the following premise:

You are detectives tasked with determining the guilt or innocence of a suspect. After interviewing the suspect, you have a list of 20 ESs to help determine the suspect’s guilt or innocence. You will analyze the data in two ways to reach a verdict: first, using an NHST approach, and second, using a Bayesian approach. Finally, you will compare the results in relation to how scientific knowledge progresses.

NHST Activity

In this activity, groups of students assign probabilities to ESs, which are then used to determine whether the null hypothesis can be rejected (i.e., determine whether the suspect is guilty or innocent). In the hypothetical scenario, the instructor should explain and/or remind students that (a) H₀ assumes innocence, and H₁ assumes guilt, (b) a p-value indicates the probability for a given ES to occur assuming the null was true, or that the suspect is innocent (i.e., p[Data = ES|H₀ = Suspect is innocent]), (c) the p-value for each statement can range between .01 (i.e., extremely unlikely assuming the suspect is innocent) and 1.00 (i.e., perfectly likely for an innocent suspect) and (d) ES must be assessed independently from others (i.e., a decision on a previous ES should not affect the decision for the next). In other words, students should be informed that all ESs should be weighted equally without being influenced by the p-values of other ESs. Provide teams with 10 minutes to assign proper p-values to each ES. For example, a team that believes ‘all criminals return to the crime scene,’ would assign a significantly small p-value (e.g., p < .05) to the ES, “The suspect was spotted at the crime scene a few days after the incident,” indicating this ES would be unlikely if the suspect were innocent.

Once a p-value has been assigned to each ES, the instructor should give teams 5 minutes to develop a strategy to decide how to use the 20 p-values to reach a final conclusion about the suspect’s innocence. Possible strategies might include counting the number of ‘significant’ ESs (p < .05), allowing ESs with extremely small p-values to sway the decision, assessing the mean/median of all the p-values, or plotting p-values under the adjacent distributions of H₀ and H₁ to estimate the overall tendency. It should be noted that this phase of the activity should be daunting as no reliable means of synthesizing p-values yet exists.

While the instructor should be aware that p-values determined by student groups to exceed .05 are insufficient to falsify the suspect’s innocence, this information should be kept concealed from students until the discussion for this portion of the activity. In an all-class discussion (10 minutes), instructors should point out the tendency that when assessing the significance of data using NHST, the value, or weight of the data are often prone to be ignored; what matters is whether or not the p-value is lower than the set α level. For example, the ES “the suspect had prior conflicts with the victim” is weighted the same as “the suspect confessed to committing the crime” to the extent that their p-values fall below .05. Although the suspect confessing would logically hold more weight than the suspect having prior conflict with the victim, NHST hardly considers this. The instructor should ask students if they believe they are making a fair and/or accurate judgment when determining the likelihood of innocence adopting the NHST approach.

Other shortcomings of NHST pointed out above should also naturally surface during team discussions. For example, at the end of the NHST activity, students will assess the significant versus non-significant p-values to determine whether the null hypothesis can or cannot be rejected, and what rejecting (or failing to reject) the null means for the suspects’ innocence. Before transitioning into the Bayesian activity, the instructor should ask students to consider if there is a more effective way of assessing the ESs to determine whether the suspect is innocent or guilty. The instructor should then explain that NHST evaluates the probability of the null for each individual evidence, incapable of synthesizing their weights or addressing multiple, competing hypotheses. That effect sizes (e.g., η²) allow for assessing and summarizing the relative strengths of multiple data and are commonly reported in addition to p-values will have to be also mentioned.

Bayesian Activity

In this activity, students reach a conclusion adopting a simplified version of Bayesian analysis. The three basic components of Bayesian analysis (i.e., prior, likelihood, posterior) must be discussed beforehand to facilitate understanding of how the approach works. Each team will start with binomial priors assuming equal probability of innocence and guilt, p(H₁) = p(H₀) = .50, to imply the initial belief is unbiased before assessing the data.

Next, the instructor should give student teams 10 minutes to read the ESs and assign the subjective likelihood, that is p(ES|H₁), or the probability for the ESs to be true if the suspect was indeed a criminal. The likelihood can be the team’s collective guesswork and should not require any serious computation. For instance, a team would find the ES, “He is an only child,” to be equally plausible whether the suspect was innocent or a criminal—the likelihood of this particular ES would then be around .50, representing that it carries no information needed to reach the decision. In contrast, the subjective likelihood should be increased dramatically to about .90 for an ES such as “The suspect confessed during the interrogation with the police,” giving more weight to this piece of data.

Finally, each team should take 10 minutes to estimate the posterior, or p(H₁|ES), which is a mathematic synthesis of the prior (p[H₁]), the likelihood of ES (p[ES|H₁]), and the “overall” probability of the ES (p[ES]). Specifically, this process uses Bayes’ Theorem (Bayes, 1763) as specified below (see Equation 1). The result at each phase represents the reallocation of the prior

belief based on the new piece of evidence.

Suppose a particular team starts with the prior (p[H₁]) at .50 (i.e., absolute uncertainty about innocence versus guilt), assesses the likelihood (p[ES|H₁]) of the first ES, “The suspect is male,” to be .70 assuming the suspect is guilty, and finds the “overall” chance for one to encounter a man as opposed to a woman in that area is no different (e.g., p[ES] = .50). Following Bayes’ Theorem, the first posterior (p[H₁|ES]) becomes .70 (i.e., [.70 × .50] ÷ .50). This posterior then serves as the new prior, based on which the likelihood and the overall probability of the second ES will be assessed to produce the next new posterior. Each team will repeat this procedure until they exhaust all 20 ESs and ultimately reach the final decision: that the suspect is innocent or guilty.

During the activity, the instructor must distinguish the likelihood from the overall probability of ES; the likelihood (p[ES|H₁]) is conditional on the suspect’s being guilty (e.g., the probability for the suspect to be male ‘assuming’ that the person is guilty), whereas an overall probability or prior (p[H₁]) applies to the whole population (e.g., the probability for a person you randomly picked from the population to be a man whether innocent or guilty).¹

Completing calculations for all ESs, students will arrive at a conclusion about the suspects’ innocence or guilt. The instructor should lead a 10-minute class discussion to compare this method to NHST, asking students to compare and contrast the methods in evaluating data. The instructor should point out that Bayesian approach has merits over NHST in that it (a) allows for synthesizing multiple data around the theory (i.e., the suspect is guilty), (b) helps estimate the probability of a theory rather than data, and (c) enables a continued update of the probability of the target theory when new data become available.

Results From Mock Data

This section presents a mock dataset to demonstrate the possible end results of the proposed activities for interested instructors. Table 1 specifies p-values, priors, likelihoods, and the posteriors for each of the 20 ESs. Results from the NHST activity can be summarized in a dot plot as shown in Figure 1 (left). The final conclusion seems difficult to make here as it requires making yet another decision; should the judgment call be made following the 3 hard evidence with p < .05 (i.e., “was spotted at the crime scene,” “has a criminal record,” “confessed the crime”), the majority votes with p = 1.00 (e.g., “has a few friends to verify his alibi,” “is 5 feet 8 inches tall,” “has a short hair”), or somewhere between the two.

Table 1.

Mock Data

Figure 1.

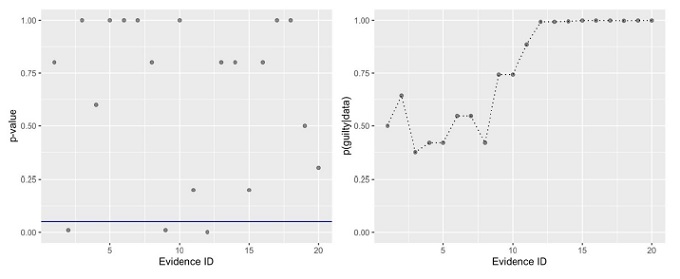
Results From a Mock NHST (Left) and a Mock Bayesian Activity (Right)Note. The horizontal line in the left plot indicates p = .05.

The process of reaching the decision should be less ambiguous after the Bayesian activity. As shown in Figure 1 (right), the posterior or p(guilty|data) is continuously updated after assessing each ES, converging to near 1.00 upon considering the 12th evidence (i.e., “confessed the crime”). Additional assessments of relatively neutral evidence (e.g., “lost his father last year”) later helped little to lower the suspicion. A guilty verdict seems reasonable.

Debriefing

The following post-activity questions can facilitate a 20-minute discussion on methodological choices, informational value of data, and advancing theory. The questions should help students consider and critically evaluate the benefits and drawbacks of each method. The instructor could also discuss how either method could be applied to different contexts or variables.

1. What about either method (NHST or Bayesian analysis) was particularly challenging to learn about? What additional information would help your understanding?
2. Compare and contrast the pros and cons of (a) assuming innocence before evaluating pieces of evidence (i.e., as you would in NHST with a null hypothesis), and (b) assuming an equal chance of innocence or guilt before collecting evidence (i.e., a Bayesian approach). How might either approach relate to the phrase “innocent until proven guilty”?
3. How did your team determine the value of each piece of evidence? What are characteristics of strong and weak evidence (e.g., source credibility, majority vs. minority opinion, data with p < .05)?
4. What do we do with ESs with a moderately low, but statistically non-significant, p-value (e.g., p = .07)? What does that tell us about the value of such studies as information? What do we learn from them?
5. How would you use both methods (i.e., NHST and Bayesian analysis) to make decisions in your everyday lives? Think about which method more closely represents the way in which empirical knowledge advances and discuss how each method affects how decisions are made.
6. Can you think of any situations in which a researcher might be testing multiple hypotheses at once? Please share. How does Bayesian analysis help us identify more credible versus less credible hypotheses? What are the potential benefits and drawbacks to testing multiple hypotheses at once?
7. Consider the following probability statements; p (spam|“free”) and p (“free”|ham or not spam), where ‘spam’ represents an unwanted advertisement message, ‘free’ denotes the appearance of the word ‘free’ in the message, and ‘ham’ refers to a legit email from a valid source. If we were to verbally describe these probability statements, what would they say? Which is an NHST probability statement, and which is a Bayesian probability statement? Which approach would be more effective to use as a spam filter to flag emails that include the word “free”?²

Limitations and Activity Adaptations

NHST is often taught as the foundational research method in many undergraduate- and graduate-level social scientific quantitative research methods courses. While one of our goals is to illustrate the utility and practicality of using Bayesian modeling in today’s data-driven environment, students may find Bayesian modeling difficult to grasp (Moore, 1997). We strongly suggest instructors ensure their students are comfortable with the two different approaches—at least the concepts associated with NHST—before beginning this activity. In addition to the NHST and Bayesian method content provided in the activity description, instructors may find it beneficial to introduce these topics in the context of human and machine learning.

Students will have a more difficult time to understand the intended lessons if confronted with the technical terms first during the activity (e.g., p-value, α-level, distribution, null vs. research hypothesis, prior, likelihood, posterior). Therefore, we recommend instructors utilize the first class session to its full extent to clarify student questions about NHST and Bayesian modeling before starting the activities.

To increase student engagement, the instructor can visually demonstrate changing Bayesian probability distributions by using twenty probability tokens, such as coins or Legos, where each token represents a 5% probability (Mueller et al., 2019). In this type of demonstration, rather than recording probabilities on paper or a whiteboard, the instructor can move the tokens back and forth between “guilty” and “not guilty” token piles to show how the probabilities of the two different hypotheses change after assessing each ES. The number of tokens moved between token piles will depend upon the perceived significance of each ES. For example, if a suspect was seen at the scene of the crime, perhaps six tokens would be moved to the “guilty” pile (i.e., assigning 30% more probability to H₁). Remind students that, in this example, the probabilities in each pile do not accurately account for the prior, likelihood, or posterior calculated in a true Bayesian analysis. Use this demonstration to simply help students visualize the process of verifying hypotheses under the Bayesian paradigm. Depending on the level of the course, the instructor could also demonstrate how to derive Bayes’ Theorem and how the equation works for real data with a finite sample size.

To adapt this activity to a hybrid course, instructors could pre-record the lecture and demonstration portions and provide the materials to students online. Then, during an in-person class, instructors could facilitate the activity with small groups of students. Finally, instructors could assign students to complete the debriefing questions asynchronously, independently or in groups, as a follow-up assignment to the activity. In a synchronous online course, each portion of the activity (i.e., lecture, demonstration, activities, debriefing) could be delivered and discussed as a large group and/or in break-out video classrooms with small groups of students.

Appraisal

In classroom trials of this activity, feedback was positive; students enjoyed discussing ES to determine the p-values in the NHST activity and moving probability tokens between “guilty” and “not guilty” hypotheses to visualize probabilities of ES in the Bayesian activity. The activity particularly helped students understand that Bayesian analysis offers a more holistic approach to evaluating data. Specifically, students learned to evaluate different ways of making predictions and realized how methodological choices can influence conclusions. Finally, students enjoyed working in small groups to collaborate, challenge, and build upon one another’s thinking.

Acknowledgments

The present research has been supported by the Research Grant of Kwangwoon University in 2020.

References

• Anderson, D. R., Burnham, K. P., & Thompson, W. L. (2000). Null hypothesis testing: Problems, prevalence, and an alternative. Journal of Wildlife Management, 64(4), 912-923. [https://doi.org/10.2307/3803199]
• Bárcena, M. J., Garín, M. A., Martín, A., Tusell, F., & Unzueta, A. (2019). A web simulator to assist in the teaching of Bayes’ theorem. Journal of Statistics Education, 27(2), 68-78. [https://doi.org/10.1080/10691898.2019.1608875]
• Bayes, T. (1763). An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S. Philosophical Transactions of the Royal Society of London, 53, 370-418. [https://doi.org/10.1098/rstl.1763.0053]
• Boster, F. J. (2002). On making progress in communication science. Human Communication Research, 28(4), 473-490. [https://doi.org/10.1111/j.1468-2958.2002.tb00818.x]
• Cohen, J. (1990). Things I have learned (so far). American Psychologist, 45(12), 1304-1312. [https://doi.org/10.1037/0003-066X.45.12.1304]
• Davis, B., Mueller, E., Sepulveda, S., Kelpinski, L., & Kappers, A., & Kim, S. (2019, April). Integrating meta-analysis into Bayesian modeling: An argument for adapting quantitative communication research methods [Paper presentation]. Central States Communication Association 2019 Annual Conference, Omaha, NE, United States.
• Domingos, P., & Pazzani, M. (1997). On the optimality of the simple Bayesian classifier under zero-one loss. Machine Learning, 29, 103-130. [https://doi.org/10.1023/A:1007413511361]
• Eadie, G., Huppenkothen, D., Springford, A., & McCormick, T. (2019). Introducing Bayesian analysis with M&M’s®: An active-learning exercise for undergraduates. Journal of Statistics Education, 27(2), 60-67. [https://doi.org/10.1080/10691898.2019.1604106]
• Granik, M., & Mesyura, V. (2017, May). Fake news detection using naive Bayes classifier. 2017 IEEE First Ukraine Conference on Electrical and Computer Engineering (pp. 900-903). [https://doi.org/10.1109/UKRCON.2017.8100379]
• Grimmer, J., & Stewart, B. M. (2013). Text as data: The promise and pitfalls of automatic content analysis methods for political texts. Political Analysis, 21(3), 267-297. [https://doi.org/10.1093/pan/mps028]
• Hu, J. (2020). A Bayesian statistics course for undergraduates: Bayesian thinking, computing, and research. Journal of Statistics Education, 28(3), 229-235. [https://doi.org/10.1080/10691898.2020.1817815]
• Kim, S. (2017). p value. In M. Allen (Ed.), The sage encyclopedia of communication research methods (pp. 1175-1177). Sage.
• Lantz, B. (2019). Machine learning with R : Expert techniques for predictive modeling (3rd ed.). Packt Publishing.
• Levine, T. R., Weber, R., Hullett, C. R., Park, H. S., & Lindsey, L. L. (2008). A critical assessment of null hypothesis significance testing in quantitative communication research. Human Communication Research, 34(2), 171-187. [https://doi.org/10.1111/j.1468-2958.2008.00317.x]
• Moore, D. S. (1997). Bayes for beginners? Some reasons to hesitate. The American Statistician, 51(3), 254-261. [https://doi.org/10.1080/00031305.1997.10473972]
• Mueller, E., Davis, B., & Kim, S. (2019, November). Methods for survival: A detective activity comparing frequentist (NHST) and Bayesian approaches. [Paper Presentation]. National Communication Association 2019 Annual Convention, Baltimore, MD, United States.
• O’Connor, B. P. (2017). A first steps guide to the transition from null hypothesis significance testing to more accurate and informative Bayesian analyses. Canadian Journal of Behavioral Science, 49(3), 166-182. [https://doi.org/10.1037/cbs0000077]
• Pek, J., & Van Zandt, T. (2020). Frequentist and Bayesian approaches to data analysis: Evaluation and estimation. Psycholog y Learning & Teaching, 19(1), 21-35. [https://doi.org/10.1177/1475725719874542]
• Popper, K. (1959). The logic of scientific discovery. Basic Books. [https://doi.org/10.1063/1.3060577]
• Ruscio, J. (2003). Comparing Bayes’s theorem to frequency-based approached to teaching Bayesian reasoning. Teaching of Psychology, 30(4), 325-328. https://psycnet.apa.org/record/2003-09372-012
• Sahami, M., Dumais, S., Heckerman, D., & Horvitz, E. (1998, July). A Bayesian approach to filtering junk e-mail. Learning for text categorization: Papers from the 1998 workshop (Vol. 62, pp. 98-105). https://www.aaai.org/Papers/Workshops/1998/WS-98-05/WS98-05-009.pdf
• Sedlmeier, P., & Gigerenzer, G. (2001). Teaching Bayesian reasoning in less than two hours. Journal of Experimental Psychology: General, 130(3), 380-400. [https://doi.org/10.1037/0096-3445.130.3.380]
• van Doorn, J., Matzke, D., & Wagenmakers, E-J. (2020). An in-class demonstration of Bayesian inference. Psychology Learning & Teaching, 19(1), 36-45. [https://doi.org/10.1177/1475725719848574]
• Westera, W. (2021). Comparing Bayesian statistics and frequentist statistics in serious games research. International Journal of Serious Games, 8(1), 27-44.https://doi.org/10.17083/ijsg.v8i1.403 [https://doi.org/10.17083/ijsg.v8i1.403]